Video
Dans la première partie, nous avons indiqué qu’un seul centime de cuivre contient environ 28 000 000 000 000 000 000 000 000 d’atomes. C’est un chiffre énorme. Si nous devions mesurer le diamètre d’un atome d’hydrogène, il serait d’environ 0,00000000000026 pouces. C’est un nombre incroyablement petit. Les chimistes utilisent régulièrement de très grands et de très petits nombres dans leurs calculs. Pour nous permettre d’utiliser efficacement cette gamme de nombres, les chimistes expriment généralement les nombres à l’aide de la notation exponentielle ou scientifique. En notation scientifique, un nombre n est représenté comme le produit de ce nombre et de 10, augmenté d’un exposant x, c’est-à-dire (n × 10ˣ). Le nombre 10² est égal à 100. Si l’on multiplie 2 × 10², cela revient à multiplier 2 × 100, soit 200. Ainsi, 200 peut être écrit en notation scientifique sous la forme 2 × 10². Lorsque nous convertissons un nombre en notation scientifique, nous commençons par écrire a le premier chiffre (non nul) du nombre. Si le nombre contient plus d’un chiffre, nous écrivons un point décimal, suivi de tous les chiffres restants. Ensuite, nous examinons le nombre pour voir par quelle puissance de 10 cette décimale doit être multipliée pour obtenir le nombre original. D’un point de vue opérationnel, il s’agit d’un déplacement de décimales. Prenons le nombre d’atomes dans une pièce d’un centime, 28 000 000 000 000 000 000 000 000 000. Nous commencerons par écrire 2,8. Pour obtenir la puissance de 10 dont nous avons besoin, nous commençons par le dernier chiffre du nombre et nous comptons le nombre de places que nous devons déplacer vers la gauche pour atteindre notre nouvelle virgule. Dans cet exemple, nous devons nous déplacer de 22 places vers la gauche. Le nombre est donc le produit de 2,8 et de 10 ²², et il s’écrit en notation scientifique 2,8 × 10 ²².
Examinons un très petit nombre, par exemple 0,00000000000026 pouces, le diamètre d’un atome d’hydrogène. Nous voulons placer notre point décimal entre le deux et le six. Pour ce faire, nous devons déplacer la virgule de notre nombre vers la droite, à treize places. Lorsque vous convertissez un nombre en notation scientifique et que vous déplacez la virgule vers la droite, la puissance de 10 doit avoir un exposant négatif. Ainsi, notre nombre s’écrira 2.6×10⁻ ¹ ³ pouces.
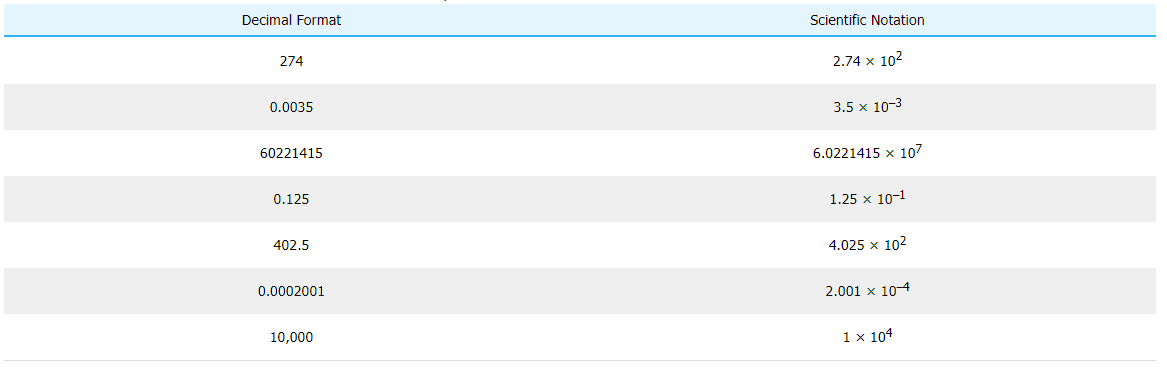
Une série de nombres au format décimal et en notation scientifique est présentée dans le tableau 1.3.1 ci-dessous.
In Part 1, we stated that a single copper penny contains approximately 28,000,000,000,000,000,000,000,000 atoms. This is a huge number. If we were to measure the diameter of a hydrogen atom, it would be approximately 0.00000000000026 inches. This is an incredibly small number. Chemists regularly use very large and very small numbers in their calculations. To enable us to use this range of numbers effectively, chemists typically express numbers using exponential or scientific notation. In scientific notation, a number n is represented as the product of that number and 10, increased by an exponent x, that is, (n × 10ˣ). The number 10² is equal to 100. If we multiply 2 × 10², we multiply 2 × 100, which is 200. So, 200 can be written in scientific notation as 2 × 10². When we convert a number to scientific notation, we start by writing the first (non-zero) digit of the number as a. If the number has more than one digit, we write a decimal point, followed by all the remaining digits. Then we look at the number to see what power of 10 that decimal place must be multiplied by to get the original number. Operationally, this is called moving decimal places. Let’s take the number of atoms in a penny, 28,000,000,000,000,000,000,000,000,000. We’ll start by writing 2.8. To get the power of 10 we need, we start at the last digit of the number and count the number of places we need to move to the left to reach our new decimal point. In this example, we need to move 22 places to the left. So the number is the product of 2.8 and 10²², and in scientific notation it’s written as 2.8 × 10²².
Let’s look at a very small number, say 0.00000000000026 inches, the diameter of a hydrogen atom. We want to place our decimal point between the two and the six. To do this, we need to move the decimal point of our number to the right, thirteen places. When you convert a number to scientific notation and move the decimal point to the right, the power of 10 must have a negative exponent. So, our number will be written as 2.6×10⁻ ¹ ³ inches.
A series of numbers in decimal format and scientific notation is shown in Table 1.3.1 below.

