Dans ce cours, nous allons explorer les techniques de base de l’analyse exploratoire des données (EDA), en nous concentrant sur les résumés statistiques et la distribution des données. Ces techniques vous permettront de développer une compréhension approfondie de vos données et de poser les bases d’analyses plus avancées.
Commençons par les résumés statistiques. Les résumés statistiques fournissent un aperçu concis des caractéristiques clés de vos données. Ils incluent des mesures de tendance centrale, telles que la moyenne, la médiane et le mode, qui indiquent où se situent la plupart des valeurs dans votre ensemble de données. Par exemple, la moyenne est la somme de toutes les valeurs divisée par le nombre total d’observations, tandis que la médiane est la valeur centrale lorsque les données sont triées par ordre croissant ou décroissant.
Les résumés statistiques incluent également des mesures de dispersion, telles que l’écart-type et l’intervalle interquartile, qui décrivent la variabilité des données. L’écart-type mesure la distance moyenne des valeurs par rapport à la moyenne, tandis que l’intervalle interquartile représente la plage de valeurs entre le 25e et le 75e percentile. Ces mesures vous aident à comprendre comment les valeurs sont réparties et à identifier les valeurs aberrantes potentielles.
Pour calculer ces résumés statistiques, vous pouvez utiliser des fonctions intégrées dans des langages de programmation tels que Python ou R, ou des outils de visualisation de données tels que Tableau ou Excel. Par exemple, en Python, vous pouvez utiliser la bibliothèque NumPy pour calculer la moyenne avec np.mean(), la médiane avec np.median(), et l’écart-type avec np.std().
(Pour aller plus loin : https://numpy.org/doc/stable/reference/generated/numpy.mean.html)

Passons maintenant à la distribution des données. La distribution fait référence à la façon dont les valeurs d’une variable sont réparties. Comprendre la distribution de vos données est crucial pour choisir les techniques d’analyse appropriées et interpréter correctement les résultats.
Les histogrammes sont un outil puissant pour visualiser la distribution des données. Ils divisent la plage de valeurs en intervalles (ou « bins ») et comptent le nombre d’observations dans chaque intervalle. La hauteur de chaque barre représente la fréquence ou la densité des observations dans cet intervalle. Les histogrammes vous permettent de voir rapidement si vos données sont symétriques, asymétriques, unimodales ou multimodales.
Les diagrammes en boîte (ou « box plots ») sont un autre outil utile pour visualiser la distribution et identifier les valeurs aberrantes. Ils résument la distribution en affichant la médiane, les quartiles et les valeurs extrêmes. La boîte elle-même représente l’intervalle interquartile, avec la ligne médiane indiquant la médiane. Les moustaches s’étendent jusqu’aux valeurs les plus extrêmes dans 1,5 fois l’intervalle interquartile, et les points au-delà sont considérés comme des valeurs aberrantes.
Pour créer des histogrammes et des diagrammes en boîte, vous pouvez utiliser des bibliothèques de visualisation telles que Matplotlib en Python ou ggplot2 en R. Ces bibliothèques offrent des fonctions flexibles pour personnaliser l’apparence de vos graphiques et mettre en évidence les caractéristiques clés de la distribution.
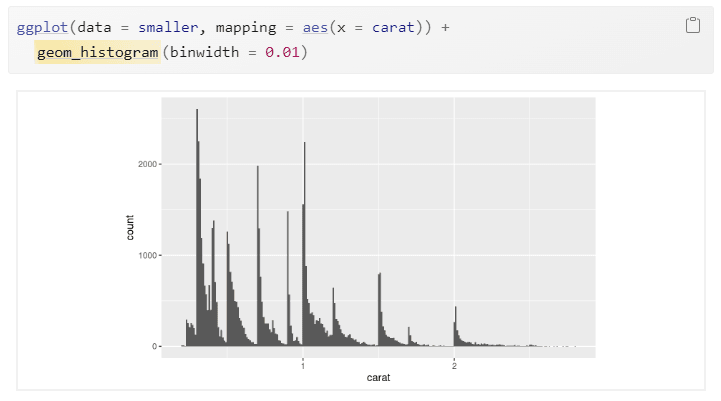
Exemple – selon R for Data Science – Garrett Grolemund, Hadley Wickham
En combinant des résumés statistiques et des visualisations de distribution, vous pouvez développer une compréhension complète de vos données. Vous pouvez identifier les modèles, les tendances et les valeurs aberrantes, et prendre des décisions éclairées sur les étapes suivantes de votre analyse.
N’oubliez pas que l’EDA est un processus itératif. Au fur et à mesure que vous explorez vos données, vous pouvez découvrir de nouvelles questions ou des problèmes de qualité des données qui nécessitent une enquête plus approfondie. Soyez curieux, posez des questions et laissez les données vous guider dans votre analyse.
En maîtrisant les techniques de base de l’EDA, vous jetterez des bases solides pour des analyses de données réussies. Vous serez en mesure de résumer efficacement vos données, de visualiser leur distribution et de communiquer vos découvertes de manière claire et convaincante. Alors, plongez-vous dans vos données, explorez et découvrez les insights qui vous attendent !
In this course, we will explore the basic techniques of exploratory data analysis (EDA), focusing on statistical summaries and data distribution. These techniques will allow you to develop a deep understanding of your data and lay the foundation for more advanced analyses.
Let’s start with statistical summaries. Statistical summaries provide a concise overview of the key characteristics of your data. They include measures of central tendency, such as the mean, median, and mode, which indicate where most of the values fall in your data set. For example, the mean is the sum of all values divided by the total number of observations, while the median is the central value when the data is sorted in ascending or descending order.
Statistical summaries also include measures of dispersion, such as the standard deviation and interquartile range, which describe the variability of the data. The standard deviation measures the average distance of values from the mean, while the interquartile range represents the range of values between the 25th and 75th percentile. These measures help you understand how values are distributed and identify potential outliers.
To calculate these statistical summaries, you can use built-in functions in programming languages such as Python or R, or data visualization tools such as Tableau or Excel. For example, in Python, you can use the NumPy library to calculate the mean with np.mean(), the median with np.median(), and the standard deviation with np.std().
(For further information:
https://numpy.org/doc/stable/reference/generated/numpy.mean.html)

Now let’s look at data distribution. Distribution refers to how the values of a variable are spread out. Understanding the distribution of your data is crucial to choosing the right analysis techniques and correctly interpreting the results.
Histograms are a powerful tool for visualizing data distribution. They divide the range of values into intervals (or “bins”) and count the number of observations in each interval. The height of each bar represents the frequency or density of observations in that interval. Histograms allow you to quickly see whether your data is symmetrical, skewed, unimodal, or multimodal.
Box plots are another useful tool for visualizing distribution and identifying outliers. They summarize the distribution by displaying the median, quartiles, and extreme values. The box itself represents the interquartile range, with the middle line indicating the median. Whiskers extend to the most extreme values within 1.5 times the interquartile range, and points beyond are considered outliers.
To create histograms and box plots, you can use visualization libraries such as Matplotlib in Python or ggplot2 in R. These libraries offer flexible functions to customize the appearance of your plots and highlight key features of the distribution.
Example – from R for Data Science – Garrett Grolemund, Hadley Wickham

By combining statistical summaries and distribution visualizations, you can develop a comprehensive understanding of your data. You can identify patterns, trends, and outliers, and make informed decisions about the next steps in your analysis.
Remember, EDA is an iterative process. As you explore your data, you may discover new questions or data quality issues that require further investigation. Be curious, ask questions, and let the data guide your analysis.
By mastering the basic techniques of EDA, you will lay a solid foundation for successful data analysis. You will be able to effectively summarize your data, visualize its distribution, and communicate your findings in a clear and compelling way. So, dive into your data, explore, and discover the insights that await you!
